問とアプローチ
細胞はすべての多細胞生物の構成要素であり、また化学反応はすべての細胞の構成要素です。 細胞という微小環境に閉じ込められた、少数だが多種の反応群は複雑かつ非線形で、また確率性の高い挙動を示します。 我々は、決定論・確率論に基づく数理理論の構築と、定量データを用いた理論の検証を通して、 様々な生体現象をどのように素過程から記述したら良いのか? 素過程を支配する物理的・化学的な性質により現象はどのように制約・拘束されているのか? 分子の少数性は現象の定性的な振る舞いにどのような影響を持つのか? 細胞などの系において平衡・非平衡系に成り立つ熱力学的法則は何か? といった問を扱っています。
01.
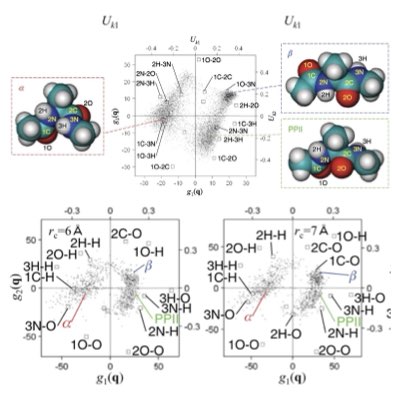
生体化学反応ネットワークの数理
多様な分子で構成される細胞内反応は一般に非線形であり、またそれぞれの分子の細胞内個数が必ずしも多くないため、高い確率性を示します。 反応系の決定論的・確率論的数理モデルやそのネットワーク構造は、多様ではあるがそれぞれは少数の分子集団から様々なロバストな細胞機能が実現されるかを理解するために不可欠な役割を果たします。 (更に学ぶには: [1], [2]).
02.
ノイジーなカスケードによるシグナルの増幅
細胞内反応に伴う確率性が有する効果の一つは、細胞現象の振る舞いを平均的な挙動からバイアスする役割です。 通常、平均化効果は単に細胞機能を損なう方向に機能しますが、全てがそうではありません。 我々はカスケード反応に内在する確率性が、特定のネットワーク構造において、入力シグナルの情報を大きく増幅することを見出し、報告しました (Learn more).
03.
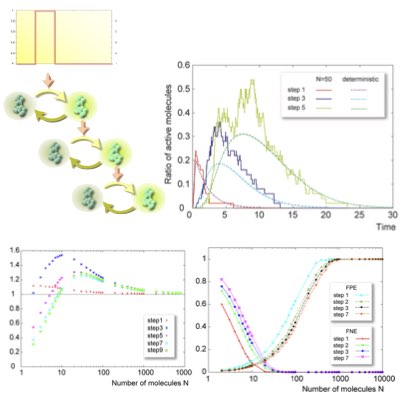
ノイズと離散性に基づく転移現象
細胞のようなミクロな反応系において、確率性やゆらぎはシステムに転移を誘導する原動力として機能する場合があります。 このノイズ励起転移、もしくはノイズ励起現象は、細胞システムが極めて大きな確率性やノイズをその構成要素である反応に内包しながらも、システムとして秩序だった振る舞いを実現できるメカニズムと関係すると考えられます。 我々はこの反応系に付随するノイズ転移現象を調べる過程で、分子の離散性に起因する新たな転移現象として、離散転移現象を発見しこれを報告しました(Learn more).
04.
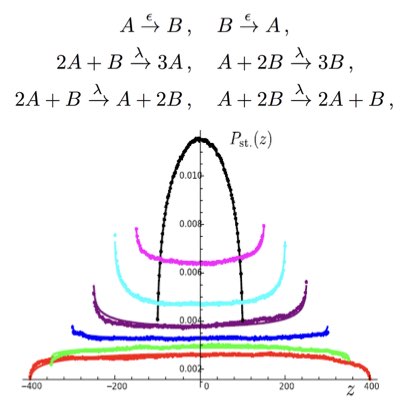
ノイズ源とフィードバックの影響を分離し計測する
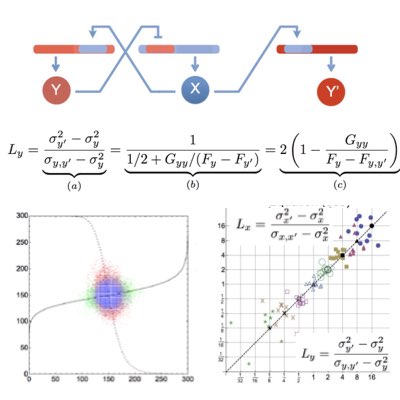
細胞内反応ネットワークにおいて、個々の反応はネットワークにゆらぎやノイズをもたらすだけでなく、ある反応で生じたゆらぎや何らかのシグナルを伝播させるという2つの機能を有します。 細胞システムのゆらぎの起源を把握するには、個々の反応の持つこの2つの機能を分離して捉えることが不可欠です。 我々はSwainとElowitzによって提案されたDualレポーター系を更に発展させ、ノイズ源と反応フィードバックの影響を分離して推定することができる新たな系、 フィードフォワード・フィードバック共役系を提案しました。またそれに付随するゆらぎ定理の存在も見出しました(Learn more).
05.
平衡化学反応系の熱力学とヘッセ・情報幾何学
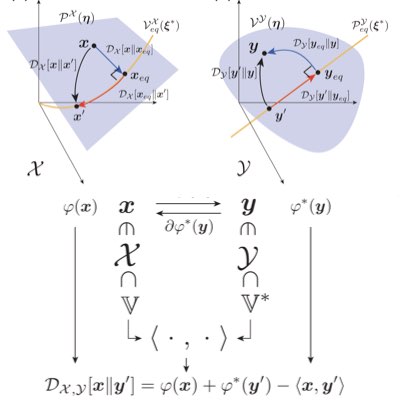
化学反応理論とその熱力学は、細胞内システムを記述し解析するための重要な数理基盤です。 しかし反応系の熱力学構造とくにその幾何学的側面を適切に捉える数理はまだ完全には成立していません。 我々は情報幾何学で活用されるヘッセ幾何学が反応系の平衡熱力学の本質を捉える方法であることを示しました。 このような理論はさらに非平衡系の理解にもつながる基礎になると期待されます(Learn more)。
06.
非平衡化学反応系のヘッセ・情報幾何学
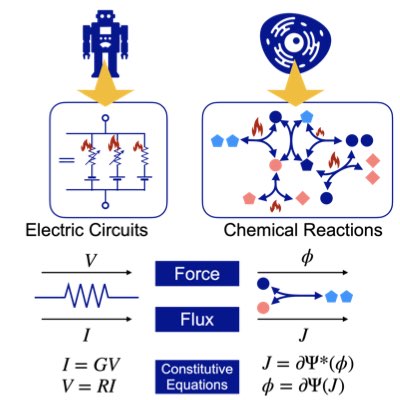
生体内のほとんどの化学反応系は非平衡です。非平衡であるがゆえに様々な機能を作り出せていると考えられています。 しかし、非平衡反応系の理論は未だ十分に確立されてはいません。 我々は平衡反応系と同じく、ヘッセ幾何学が非平衡な反応系においても本質的な役割を果たしていることを見出しました。 そしてさらに、平衡・非平衡をつなぐ反応熱力学の幾何学理論を構築しています(Learn more)。
07.
成長を伴う自己複製過程の熱力学
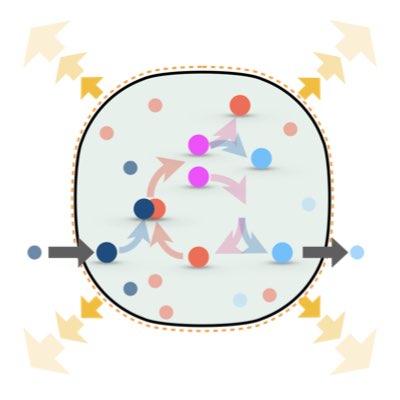
生きている物理系とそれ以外の物理系を隔てる本質的な差異の一つは自己複製能にあります。 自己複製能は、生きている物理系としての非平衡状態を維持する原動力でもあります。 しかし、自己複製によって駆動される非平衡状態がどのような典型的な振る舞いを有するのか、 またそれはエネルギーや物質の定常流で維持される非平衡状態と何が違うのか?は未解明です。 我々は自己複製反応と体積変化が共役する反応系の熱力学を確立し、この課題を扱う路を開拓しました(Learn more)。
08.
人工遺伝子スイッチにおける遅れと安定性
遅れは細胞内ネットワークに遍在する性質の一つであり、ネットワークの安定性や振る舞いを劇的に変える可能性があります。 我々は、数理的手法に基づき、正のフィードバックしか持たない遺伝子ネットワークの漸近的な安定性は時間遅れによって影響は受けないことを示しました。 この結果は遺伝子スイッチが持つべき安定性を実現するための十分条件を与えます。 この結果と並行して我々は、時間遅れに影響されない安定性を持つ人工遺伝子スイッチを設計する方法を提案しました。 (Learn more).
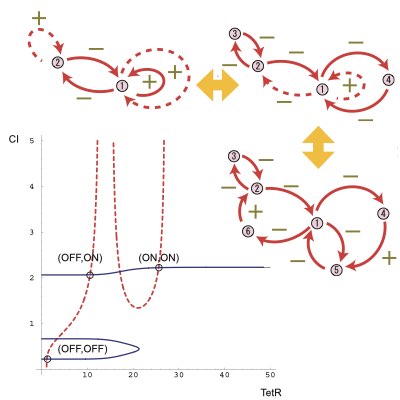
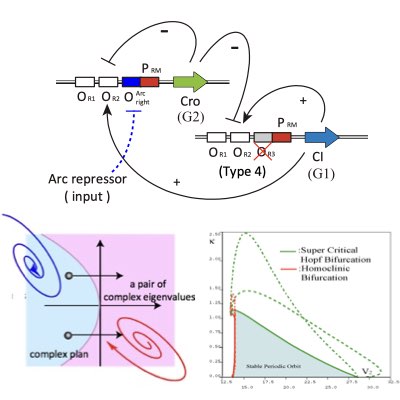
09.
人工遺伝子振動子の設計
振動は異なる細胞プロセスを同期し、協調的に機能させる細胞内の動的構成要素の一つです。 適切な性質をもつ振動を設計しまたそれを制御することは、細胞の大域的な性質を変調させることに役に立ちます。 我々は、分岐理論を用いることで、ロバストな振動を示す人工遺伝子振動子を設計する方法を提案しました。
10.
大きな構造変化をタンパク質に誘導する摂動の設計
タンパク質の構造とそのゆらぎは、タンパク質の機能を決定する重要な要因です。 したがって、構造を適切に制御しデザインする方法は分子工学の重要な課題と考えられます。 しかし、どのようにしてタンパク質の構造の機能的な差異を定量化すればよいのか、そしてどんな意味でタンパク質に変化を誘導する摂動を設計するのかは明らかではありません。 我々は、タンパク質の構造ゆらぎに関するKL情報量を、ゆらぎを含めたタンパク構造の差異を測る測度としてもちいることを提案しました。 また、KL情報量の情報論的性質を用いることで、構造ゆらぎの意味で大きな変化をタンパク質に誘導する最適な摂動を設計する方法を新たに提案しました。 (Learn more: [1], [2]).