問とアプローチ
生体システムは個体から細胞まで積極的に環境の情報を取得・処理し、運動・状態変化などの応答を決定します。 しかし、ミクロな細胞を構成する化学反応は極めて確率的でノイジーです。また生命が直面する環境は広大で不確定に変化します。 にもかかわらず、しばしば生命システムは極めて巧みな振る舞いや物理限界に近い機能性を示します。 生体システムが、確率的な素過程をもとにどのように環境の情報を取得・処理し、そしてその情報をどう活用しているのか。その原理は未だ明らかでありません。 我々は情報理論や情報熱力学をベースとして、動的に変化する環境の認識や探索に関する数理理論の開発や生体情報処理の最適性を扱う理論の構築を行っています。 またそれを定量的な計測と組み合わせて、生体情報処理を情報の観点から理解することを探求しています。
01.
細胞によるノイジーなシグナルの処理
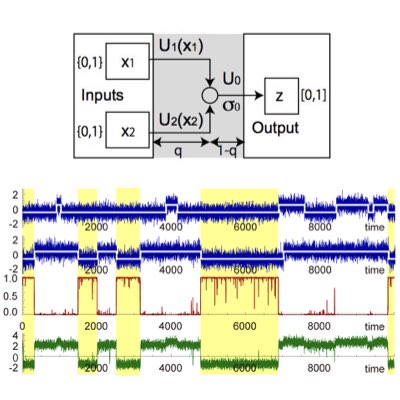
細胞が、確率的に振る舞う受容体を介して環境を感知することは、必然的に環境情報の大きな劣化をもたらします。 にも関わらず、幾つかの現象において、細胞は環境状態のダイナミックな変化に対して、極めて忠実に応答できることも確認されています。 この観測は、細胞が受容体を介したノイジーなシグナルから何らか環境の情報を抽出できていることを示唆します。 我々は、逐次ベイズ推定の理論を活用して、ノイジーな受容体シグナルから2値的な環境変動の情報を最適に復号する反応ネットワークを導出しました。 また、このネットワークが自己活性能を持つリン酸化・脱リン酸化サイクルで実現できることも明らかにしました(Learn more: [1], [2]).
02.
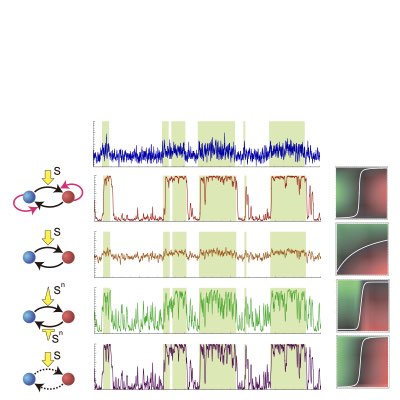
自己活性的な綱引き反応によるベイズ推定の生体実装
あるネットワークが、ノイジーなシグナルからのベイズ復号を実現するために必要な本質的な性質は、自己強化的な性質を持つ綱引き構造とその綱引きがノイジーなシグナルでバイアスされることにあることを明らかにしました。 この解釈を活用することで、ノイジーなシグナルからのベイズ復号を実装するネットワークとして、自己誘導能のある分岐型の分化プロセスや、極性分子を自己活性的に取り合うを極性形成反応を複数提案しました。 (Learn more: [1], [2]).
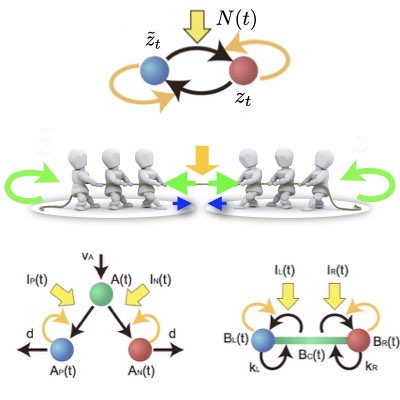
03.
動的ベイズ推定とノイズ励起現象の関係
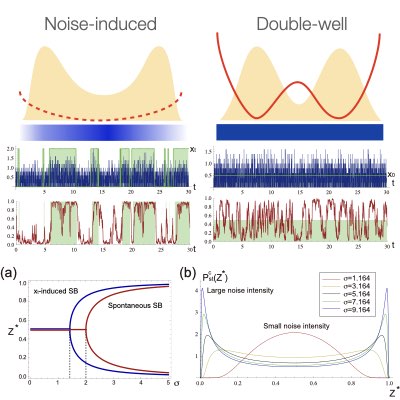
ノイズに埋もれたシグナルを復号するためには、ノイズへの不感受性と埋もれたシグナルへの感受性を両立しなければなりません。 自己活性能をもつリン酸化・脱リン酸化サイクルや綱引き構造は、どのようにしてこの背反する性質を実現しているのでしょうか? 我々は、この2つの性質を両立させるダイナミクスが、ノイズ励起転移にあることを明らかにしました。 更に我々は、ノイズ励起転移の存在を同定するための計測手法の提案も行いました。 (Learn more: [1], [2])
04.
動的でノイジーな情報処理の数理
細胞や個体が直面する環境の変動は、2値的変動とは比べ物にならない複雑さと時間的な階層性を有します。 逐次ベイズ推定の方法をさらに拡張することで、我々は大腸菌や細胞性粘菌の化学走性において観測されている極めて高い勾配感知能に関連すると思われるネットワーク構造を導出しました。 この結果は、時間センシング・空間センシングを統合するもので、動的な細胞情報処理の基礎となると期待されます。
05.
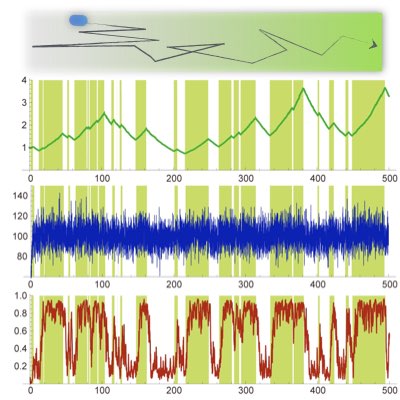
大腸菌走化性ネットワークの最適性
上記で導いたような最適な情報処理機構は本当に実際の生物の中に存在するのでしょうか? 我々は、大腸菌走化性を実現する反応ネットワークの物理化学モデルが、最適フィルターにより導かれた方程式と完全に一致することを見出しました。 また、実験計測されていた走化性のフィードバック関数が、最適フィルターの理論予測により再現されました。 この結果は細胞情報処理が最適な構造を有していることを示唆しています(Learn more).
06.
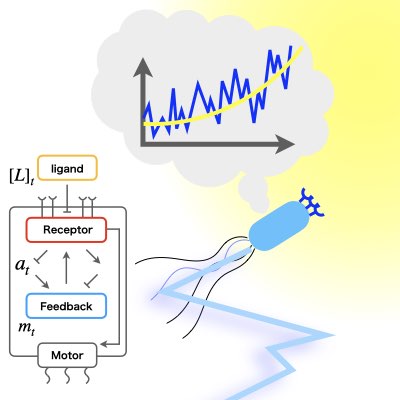
最適な走化性の感知と制御
生体は環境中の情報を感知するだけでなく、その情報を元にして自身の運動を制御し環境を探索します。 生体の制御機構は高いノイズと非線形をもち、広く使われている線形制御理論で扱うことは難しいです。 我々は、部分観測最適制御理論とKullback-Leibler制御を組み合わせ、生体のRun-Tumble走性を扱いうる理論を構築しました。 このような理論は様々なタイプの生体探知機構の最適性を扱う理論的 基礎になると期待されます(Learn more).
07.
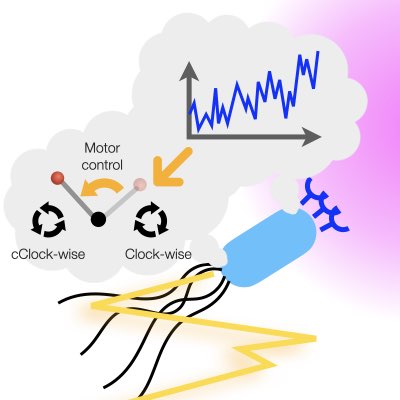
リソース制約下での最適制御理論
生体システムは極めて限られたメモリーや確率的に振る舞いをする素子により様々な情報処理や制御を実現します。しかしこのような制御側の制約を扱う適切な理論が有りませんでした。 我々は平均場制御などの数理的技法を使い、制御側や情報処理側の記憶容量や不確実な挙動を考慮することができる数理理論を構築しました。 この理論を活用・発展することで、活用できるリソースの変化に依存した情報処理の戦略の変化など様々な問題が扱えるようになると期待できます(Learn more).
08.
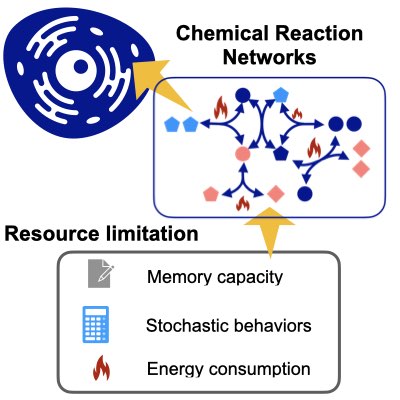
動的ベイズ理論に基づくノイズ耐性ゲートの設計
近年、ロジック回路の微細化と低消費エネルギーへの要求に伴い、各種論理演算を極めて高いノイズ環境下で安定に実現させることが重要になってきています。 生物がノイジーな構成要素を用いて安定な振る舞いを実現するそのメカニズムにヒントを得て、我々は高ノイズ環境下で機能しうる論理ゲートの理論実装を提案しました。 我々の結果は、ベイズ的な方法をコンピューターアーキテクチャーの高次レイヤーだけでなく、物理層かそこに近い低次レイヤーでも用いることの重要性を示唆しています(Learn more).