問とアプローチ
生体システムは不確定に変動する環境に柔軟に適応する能力を有します。 自然選択に基づくダーウィン進化は、環境適応の基本メカニズムの一つであり、生体は集団内に遺伝型・表現型の多様性を生成することで、未知の環境変動へのリスクを分散し、生存確率や適応度を高めます。 また、自己複製する生体が選択という過程をへることにより本来物理的には稀であるはずの生きている状態が保たれます。 進化動態により、生物の典型的なあり方や性質がどのように規定されているのでしょうか? また自然選択が働くための必要条件としての自己複製は、どのような条件で実現するのでしょうか? 我々は進化動態によって駆動・維持される生命システムの性質を扱う理論の構築に取り組んでいます。 また生体は進化によって適応するだけでなく、各細胞・各個体レベルで環境を積極的に感知・予測し、事前に適応的な状態を選択することのできる脳の様な器官を発達させてきました。 この2つの適応機構は進化動態全体にどのように関連しているのでしょうか? 我々はダーウィン的自然選択と予測的情報処理に共通する情報論的変分構造を用いて、この2つの適応機構を理論的に統合し、 生物に適応関する統一的な理論の構築とその応用にも取り組んでいます。
01.
自然選択によりバイアスされる内在ダイナミクス
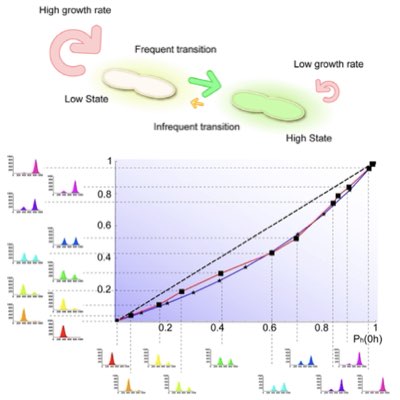
細胞内反応の確率的挙動は、遺伝的に均一な集団にも表現型レベルでの多様性をもたらします。 しかし、集団に見られる多様性は必ずしも個々の細胞の持つ内因的な確率性を反映するわけではありません。 特に、個々の細胞の表現型が何らかの選択圧に晒されている場合はなおさらです。 我々は細胞集団の定常状態への緩和ダイナミクスを定量的実験計測し、それを数理モデルと組み合わせることで、 集団レベルで見ると、人工遺伝子スイッチ(トグルスイッチ)の安定性が選択によって大きくバイアスされて、 内因的な安定性と全く異なって見えることを示しました。 この結果は選択の存在下において、1細胞レベルの挙動と集団レベルの挙動に生じうる乖離を実験的に明らかにしています(Learn more).
02.
集団ダイナミクスに内在する熱力学的変分構造
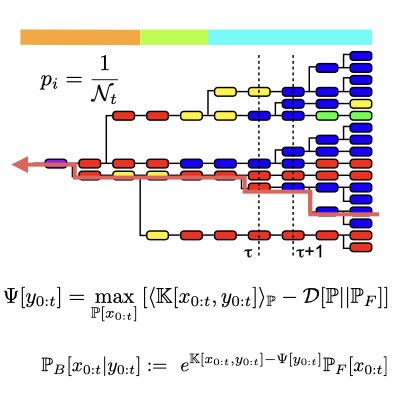
多様性を持つ細胞集団に於いて、1細胞レベルの挙動と集団レベルでの挙動の関係は必ずしも完全に理解されているわけではありません。 我々は、経路積分表現を用いて細胞群動態を記述することで、自然選択による集団への影響は、個々の細胞を時間前向きに見たときの経路の挙動と、 時間後ろ向き(遡及的)に見た時の経路の振る舞いの差として表せることを明らかにしました。 更に、経路レベルで現象を表すことで、集団動態に内在する変分構造を同定し、この構造が熱力学や情報理論、ベイズ統計にける変分構造と数学的に等価なものであることも示しました。 (Learn more and more).
03.
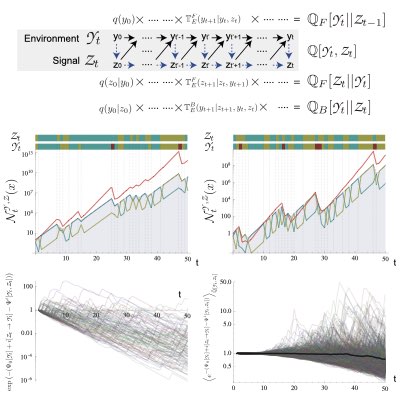
事後的な情報処理としての自然選択
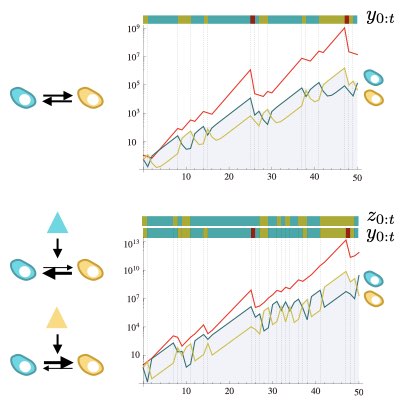
集団動態と情報理論に共通して見ら得る変分構造を活用することで、我々は自然選択による適応が、ある種の情報処理とみなせることを明らかにしました。 より具体的には、選択を遡及的な経路レベルで見ることで、ある種の情報圧縮(レート歪理論)と等価であることを示しました。 この結果は、選択を事後的(遡及的)な情報処理を捉える数学的な基礎を与え、又同時に、予測的・事前的な適応と、自然選択に基づく事後的な適応を統合する手段を与えてくれます。 この方法により、我々は環境を観測し、予測的に環境に適応することで得られる適応度利得が、環境の観測によって得られる情報と結びつく一般的な関係を明らかにしました。 (Learn more: [1], [2]).
04.
適応度と情報のゆらぎ定理
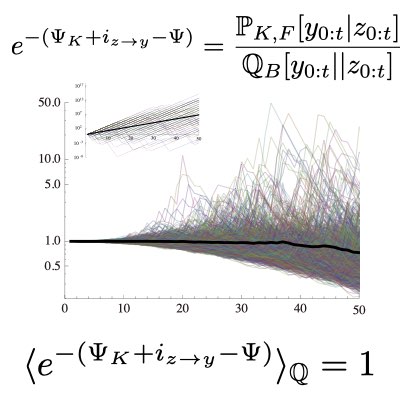
集団動態や自然選択下の適応を考える上で、遡及的な経路は、確率熱力学における時間反転経路と同じような役割を果たします。 この関連を活用して、我々は変動環境下における適応度のゆらぎと、変動環境を観測して得られる環境情報の情報量との間に、各種のゆらぎ関係(ゆらぎ定理)が成り立つことを示しました。 進化生物学的な観点から、このゆらぎ定理は進化適安定戦略(ESS)の極めて単純なversionを、確率変動下に拡張したものと捉えることができます。 この拡張されたESSは、変動環境下において平均的に適応度を最大にする最適戦略に対して、環境ゆらぎを利用することで、確率的に平均最適戦略を有限時間で優越しうる非最適戦略が常に存在することを示しています。 つまり、変動環境下で絶対に最適な戦略は存在し得ないことがわかりました(Learn more and more).
05.
ハウスキーピング適応度と余剰適応度
ヘテロな集団の実際の増殖(適応度)は、どんな環境変動が実現したか、に強く依存します。 環境を変動させて、細胞などの集団の増殖を制御するためには、環境変動と集団の応答(特にその増殖率)の関係を理解する必要があります。 我々は、集団動態の経路積分表現を用い、環境変動による増殖(適応度)の変動をハウスキーピング適応度と余剰適応度に分解しました。 集団動態と定常熱力学との数学的な関係性を活用することで、我々は余剰適応度に対して、1細胞レベルの挙動が詳細釣り合いを満たす時に、クラウジウス不等式と類似の関係性が成り立つことを明らかにしました。 我々は結果は、個々の細胞の持つ内因的な動態の非平衡性が、細胞集団増殖の制御を実現する上で極めて需要な役割を果たすことを明らかにしました。 (Learn more).
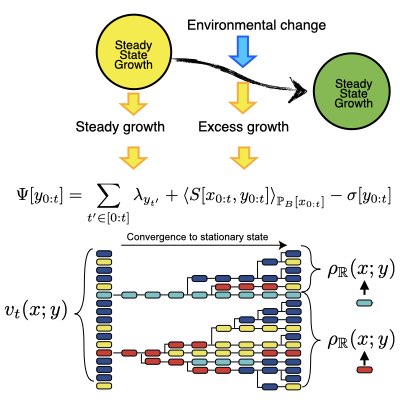
06.
分岐過程と適応度応答関係
集団動態の経路積分表現における時間前向き、時間後ろ向きの動態の特徴化は、有限サイズ集団のモデルにおける分岐過程や祖合過程と強く関連しています。 我々は連続時間多状態分岐過程の経路表現にセミマルコフ過程の理論を組み合わせ、時間前向き・後ろ向き動態の大偏差理論と関係を明らかにするとともに、 その応用として系譜から計測された量から適応度の応答性を予測する方法を構築しました。 このような手法は実際の系譜データから集団動態の方向性を予測する基盤となります。 (Learn more).
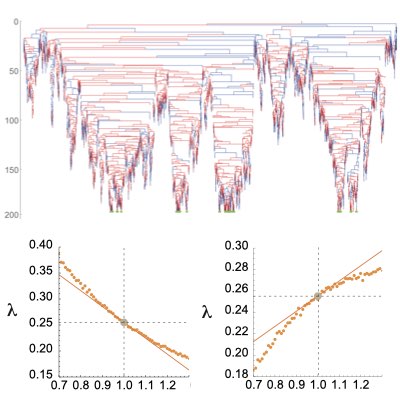
07.
細胞系譜データからの細胞隠れ状態の推定
細胞の増殖動態は個々の細胞の遺伝系のみならず表現型の状態に強く依存します。 どのような表現型の細胞が集団内にどれくらい存在しどのように変化しているのかの情報は、集団の動態や薬剤応答などを予測するのに不可欠です。 しかしそのような表現型状態を計測することは一般に困難です。我々は逆に計測された系譜情報の個々の細胞の増殖動態の性質から、 細胞の持つ隠れた(観測されていない)表現型状態を推定する手法(Lineage EM algorithm)を構築しました。 この手法により大腸菌集団において、世代間時間を超えて変動する遅い隠れ状態成分などを同定しました。 我々は結果は、系譜データ解析技術の基盤になると考えています。 (Learn more).
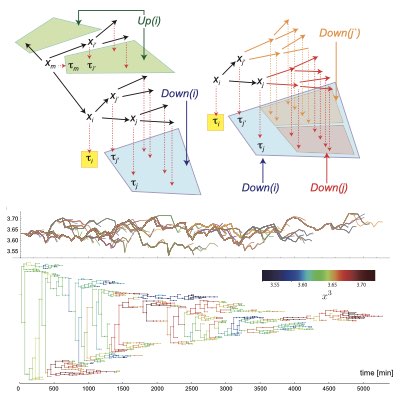
08.
個々の細胞の情報処理とその進化的価値
多くの生物は、自然選択により集団として様々な環境に適応するだけでなく、個々の細胞や個体が積極的に環境を感知し、個として適応的に振る舞う機構を持っています。 このような個の情報処理機構は進化的にどれだけの価値を持つのでしょうか? 我々は適応度と情報量のゆらぎ定理を拡張し、個の情報処理のもつ適応的価値は情報処理により得られる情報量を優越しうることを明らかにしました。 この結果は個と集団の適応の関係を統一的に理解するための第一歩になると考えています。 (Learn more).
09.
集団の進化過程と個の学習の関係性
進化は新規変異の発生とその選択による集団レベルでの適応過程です。 一方多くの生体システムは、自身やその祖先の経験などから学習をして振る舞いをかえる個として適応を示します。 我々は集団の進化と個の学習を統一的に扱う理論を構築しました。 その理論を用いて、祖先の情報から学習する祖先学習が本質的に進化を加速することを示し、 また定量的に進化と学習の関係を解析する拡張されたフィッシャーの基本定理を提案しました。 このような方法は、学習と進化のさらなる理解につながります。 (Learn more)。
10.
神経科学と進化生物学を統合する
神経科学と進化生物学は、それぞれ生物学における主要分野の一つです。 この2つは生物システムがもつ適応能とそのメカニズムが主要な研究対象であるにも関わらず、適応のメカニズムと時間スケールが大きく異なっていたため、歴史的には比較的独立に研究が行われてきました。 しかし、癌や免疫などの代表されるように、2つの異なる適応メカニズム、予測的な適応と自然選択による適応、の2つが絡み合う現象も次々に見出されています。 我々は、異なる適応メカニズムを統合する我々の理論をベースとして、これら2つの領域をつなぐ研究ができるのでないかと考えています。